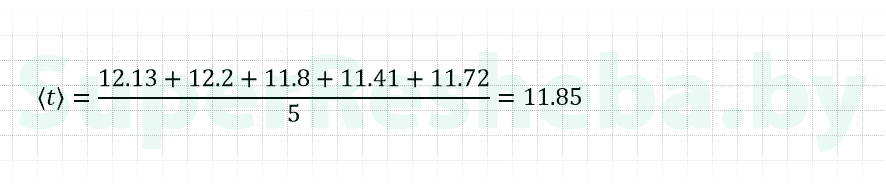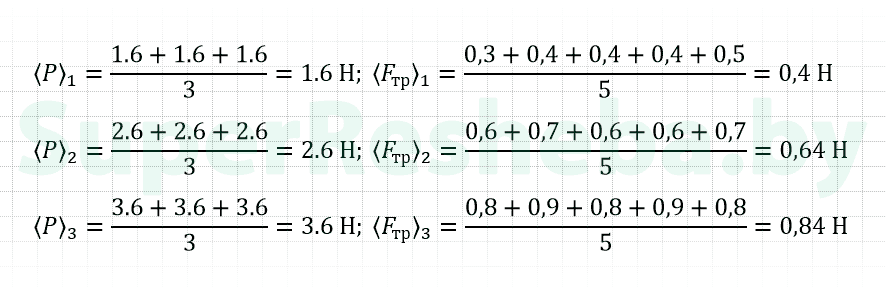3. Рассчитайте и занесите в таблицу среднее значение промежутка времени <t>, за который шарик совершает N = 10 оборотов.

4. Рассчитайте и занесите в таблицу среднее значение периода вращение <T> шарика.

5. По формуле (4) определите и занесите в таблицу среднее значение модуля ускорения.

6. По формулам (1) и (2) определите и занесите в таблицу среднее значение модулей угловой и линейной скорости.

Опыт	N	t	T	a	ω	v
1	10	12.13	—	—	—	—
2	10	12.2	—	—	—	—
3	10	11.8	—	—	—	—
4	10	11.41	—	—	—	—
5	10	11.72	—	—	—	—
Ср.	10	11.85	1.18	4.25	0.63	0.09

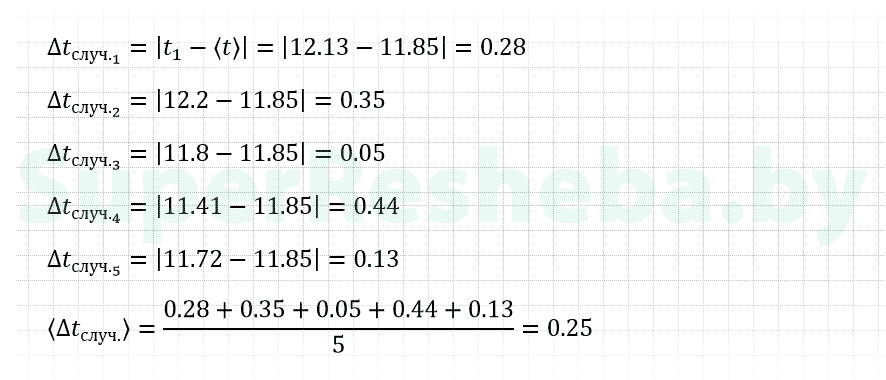
7. Вычислите максимальное значение абсолютной случайной погрешности измерения промежутка времени t.

8. Определите абсолютную систематическую погрешность промежутка времени t.

9. Вычислите абсолютную погрешность прямого измерения промежутка времени t.

10. Вычислите относительную погрешность прямого измерения промежутка времени.

11. Запишите результат прямого измерения промежутка времени в интервальной форме.

Ответьте на контрольные вопросы

1. Как изменится линейная скорость шарика при его равномерном вращательном движении относительно центра окружности?

Линейная скорость характеризуется направлением и величиной (модулем). Модуль — величина постоянная, а направление при таком движении способно изменяться.

2. Как доказать соотношение v = ωR?

Так как v = 1/T, связь циклической частоты с периодом и частой 2π = VT, откуда V = 2πR. Связь линейной скорости и угловой 2πR = VT, отсюда V = 2πr/T. (R — радиус описанной, r — радиус вписанной)

3. Как зависит период вращения T шарика от модуля его линейной скорости?

Чем выше показатель скорости, тем меньше показатель периода.

Выводы: научился определять период вращения, модули, центростремительного ускорения, угловую и линейную скорости при равномерном вращении тела и рассчитывать абсолютную и относительную погрешности прямых измерений промежутка времени движения тела.

Суперзадание

Определите ускорение материальной точки при её равномерном вращении, если за Δt = 1 с она прошла 1/6 длины окружности, имея модуль линейной скорости v = 10 м/с.

Длина окружности:

S = 10 ⋅ 1 = 10 м
l = 10⋅ 6 = 60 м

Радиус окружности:

r = l/2π
r = 6/2 ⋅ 3 = 10 м

Ускорение:

a = v2/r
a = 1002/10 = 10 м/c2.